Conceptos fundamentales de la Geometría

PUNTOS 

Un punto sólo tiene posición en el espacio.Es la unidad indivisible de la geometría.No tiene dimensión (largo, alto, ancho) es cero dimensional.

ejemplo punta de un lápiz

LINEAS 

Es una figura geométrica que se genera por un punto en movimiento.

Si el punto se mueve sin cambiar de dirección, entonces es una línea recta , solo tiene longitud es uni-dimensional

ejemplo: el borde de una regla.

 .

PLANO 

Un plano es una superficie que tiene longitud y anchura pero no espesor.
El plano tiene dos dimensiones a diferencia de la mayoría de los casos que nos rodean que están en tres dimensiones.
ejemplo de plano parte superior de un escritorio

Puntos y lineas en el plano

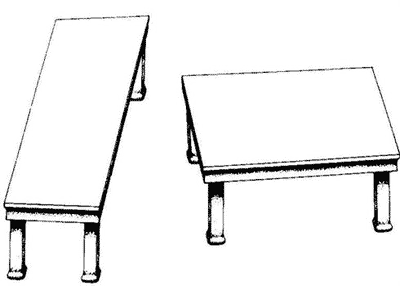
• des de un punto en el plano puede originarse una serie infinita de lineas. 

• En una porción de plano existe infinitos puntos.

las lineas se clasifican en rectas y curvas, pero al combinarse estas, se obtienen orto tipos de lineas que se conocen como:

• linea quebrada es una combinación de porciones de lineas rectas.

• lineas mixtas es una porción  de lineas rectas y quebradas.

• cuando las lineas quebradas y mixtas tienen sus extremos separados, se denominan abiertas; si sus extremos coinciden, se denomina cerradas.

• linea entre dos puntos: 

si colocan dos puntos en un plano, por ellos podrán pasar infinitas lineas curvas pero solo podra pasar una sola linea recta.

• lineas horizontales, verticales y oblicuas.

las lineas atendiendo a su posición en el plano, se clasifica en: verticales horizontales y oblicuas.

• linea vertical : es aquella que sigue la trayectoria de cualquier objeto pesado que se deje caer libremente. un ejemplo podría ser la linea que se forma en la intersección de dos paredes.

• linea horizontal : es aquella que no tiene inclinación alguna. la linea que se forma en la intersección de una pared  con el piso,  brinda la idea de una linea horizontal.

.

• linea oblicua: es aquella que tiene una inclinación sin llegar nunca a ser vertical ni horizontal.

Iris Noriega

La Semirrecta.

Si sobre una recta se marca un punto de manera que la separe en dos partes, cada una de las porciones resultantes recibe el nombre de semirrecta.

 

La semirrecta es una porción de recta que está limitada en un extremo por un punto llamado origen, y por el otro sentido es ilimitada.

 La semirrecta tiene una sola dirección y un solo sentido.

Las semirrectas al estar unidas por el origen, se denominan: consecutivas y adyacentes.

Semirrectas consecutivas: Tienen el origen común.

Semirrectas Adyacentes: Tiene el origen común y son de sentidos opuestos.

Si colocamos un punto en un plano, por este punto se pueden originar infinitas rectas.

Las semirrectas tienen una dirección de acuerdo de acuerdo con su posición, por ejemplo: horizontales, verticales y oblicuas.

El Segmento.

Es una posición de línea recta limitada por dos puntos llamados extremos.

CLASES DE SEGMENTOS.

El segmento es limitado por los extremos tal como lo dice su definición; tiene además una dirección horizontal, vertical u oblicua. El segmento no tiene sentido.

A-Segmento consecutivo: tienen un extremo en común.

B-Segmentos Adyacentes: Tienen un extremo común y pertenecen a la misma línea recta.

C-Segmentos Incidentes: Tienen un punto común que no es ninguno de sus extremos.

D-Segmentos Disyuntos: Son aquellos que no tienen ningún punto en común.

Gabriela Cañate. 8-885-1020.

Comparación de Segmentos

Por definición, medir es comparar dos magnitudes; si medimos o comparamos segmentos, éstos pueden: Mayor que (>), Menor que (<) o igual (=).

Ejemplo:

Estas tres situaciones son exclusivas, es decir, si se cumple una, se excluyen las otras dos.
Ejemplo:

Si afirmamos que:

AB es menor que CD, de ninguna manera podría resultar que AB  sea mayor que CD y tampoco que sea iguales. Lo mismo sucede para cada uno de los otros casos.

Adición de Segmentos

Para la adición de segmentos se coloca uno a continuación de otro de manera que sea adyacentes, y se toma la medida que va del primer extremo del primer segmento al segundo extremo del ultimo segmento.

Ejemplo: 

Sustracción de Segmentos

Para la sustracción de segmentos, s coloca el segmento sustraendo, sobre el segmento minuendo, haciendo coincidir sus extremos finales; el segmento resultante representa la diferencia. Se restan los segmentos AB - CD se coloca CD sobre AB, haciendo que coincidan los extremos C con B; entonces el segmento resultante AD representa la diferencia .

Práctica No. 1

I. Llena los espacios con las respuestas correctas.

1. Conceptos fundamentales de la geometría: línea, punto, superficie.

2. Atendiendo a su dirección o posición, las rectas puede ser: horizontal, vertical, oblicua.

3. Dos clases de líneas: rectas, curvas.

4. Dos combinaciones de líneas: quebradas, mixtas.

5. Si las líneas se tocan en sus extremos, se llaman: cerradas.

6. Por un punto puede pasar infinitas líneas.

7. Semirrectas con origen común y sentidos opuestos adyacentes.

8. Atendiendo a la Unión o no de sus extremos, y a su posición, los segmentos se clasifican en: consecutivos, adyacentes, incidentes, disyuntos.

9. Al comparar dos segmentos, se puede presentar una de tres situaciones que son: mayor que >, menor que <, igual que =.

10. Por dos puntos pasa una sola línea recta.

11. En un plano se originan infinitas Semirrectas.

II. Pareo
Escribe sobre la raya de la columna de la derecha el número correspondiente de la columna izquierda.

1. Combinación de porciones de la líneas rectas             __8__ línea
2. Segmentos que no tienen ningún punto en común     __6__ semirrectas
3. Semirrectas con origen común y sentidos opuestos   __12__ segmento
4. No tienen longitud ni anchura ni altura.                     __7__ línea mixta                  
5. Línea que no tiene inclinación.                                  __14__ segmentos incidentes
6. Tiene una sola dirección y un solo sentido.                __3__ semirrectas adyacentes

7. Combinación de porciones de líneas rectas y curvas  __13__ Euclides

8. Solo tienen una inclinación.                                         __1__ línea quebrada
9. Semirrectas con origen común.                                    __15__ medir
10. Líneas que tienen una inclinación.                             __11__ superficie
11. No tiene espesor, solo largo y ancho.                         __5__ línea horizontal
12. Porción de líneas recta limitada por dos puntos
       Llamados extremos.                                                    __2__ disyuntos
13. Autor del libro "los Elementos"                                   __10__ línea oblicua
14. Segmentos que tienen un punto en común que
       No es ninguno de sus extremos.                                  __9__ semirrectas consecutivas
15. Comparar dos magnitudes.                                           __4__ punto



III. Identifica las gráficas que se dan y coloca su nombre sobre las líneas punteadas.



1. Atendiendo a su forma, escribe el nombre de cada figura y clasifícala en abierta o cerrada.

2. Basándose en su definición, escribe cómo son los Segmentos:

   

3. Atendiendo a si dirección o posición, escribe el nombre de las siguientes líneas:

4. Identifica cada línea con su nombre:

BEYRA BUSTAMANTE
8-743-1886

EL ÁNGULO

   El ángulo es la porción del plano limitado por dos semirrectas con origen común, en donde las semirrectas reciben el nombre de lados.   El origen común de las dos semirrectas recibe el nombre de vértice y, generalmente, se designa con la letra O .

1.  Ángulo cóncavo y convexo

Ángulo convexo:  Es el que está comprendido entre los lados o semirrectas del ángulo.

Ángulo cóncavo:  Es el que al prolongar sus lados por el origen común, contiene  a dichas prolongaciones.

2.  Ángulos concecutivos y adyacentes 

Cuando un ángulo tiene un lado y el origen común con otro ángulo, se dice que son ángulos consecutivos.   Se afirma que varios ángulos son consecutivos, si el primero  es consecutivo con el segundo; el segundo es consecutivo con el tercero y así sucesivamente.

Cuando dos àngulos tienen origen comùn y además sus lados no comunes son semirrectas opuestas, estos àngulos se denominan àngulos adyacentes.

3.  Mediciòn de àngulos

Medir un àngulo es comparar su amplitud con otra amplitud que se toma como unidad de medida. La amplitud o medida de un ángulo queda determinada por la extensión de plano comprendida entre los lados del ángulo. 

Yarideth Toribio

Cédula: 3-705-1207

 

ELIZABETH PÉREZ

3-108-639

Angulo agudo .es el que mide menos de noventa grados.

Clasificación de los ángulos atendiendo a su amplitud.

Según su amplitud los ángulos se clasifican así,. angulo agudo, obtuso,recto,llano y angulo de giro.

angulo agudo.

Angulo obtuso.Es aquel mas de noventa grado y menos de 180 grado.

                                

    Angulo recto. Es el que mide noventa grado

Angulo llano, Es el que mide ciento ochenta grado.

                                                         

                                                                

Angulo de giro,  Es el que mide tresciento sesenta grados.

Suma y Resta de Angulos,

Suma de Angulos, Para sumar dos angulos se coloca uno a continuaion del otro,tal como los angulos consecutivos, y se mide tomando la medida desde el lado inicial del primer angulo hasta el lado final del ultimo angulo.

Resta deAngulos.  

Pra restar dos angulos se colocan de maneraque el angulo a restar queda dentro del angulo mayor, de tal forma coincida sus lados iniciales, luego se mide la amplitud del lado final del angulo restado al lado finaldel angulo del cual se resta.

La bisectriz

La bisectriz de un angulo es la semirrecta que tiene como origen el vértice y divide  al angulo en dos  ángulos iguales.





Ángulos Complementarios y Suplementarios.

Ángulos complementarios: cuando la suma de dos ángulos es igual a noventa grados, los ángulos son complementarios. La suma de dos ángulos complementarios es igual a un ángulo recto.

El complemento de un ángulo es la amplitud que le falta a ese ángulo para completar un ángulo recto.

  

Ángulos Suplementarios: Si la suma de dos ángulos  es igual a ciento ochenta grados, los ángulos son suplementarios. La suma de dos ángulos suplementarios es igual a un ángulo llano.

El suplemento de un ángulo es la amplitud que le falta a ese ángulo para completar un ángulo llano.

Practica.

① Define los siguientes conceptos.

1.      ANGULO ADYACENTE: Cuando dos ángulos tienen origen en común y además sus lados comunes son semirrectas opuestas.

2.      ANGULOS COMPLEMENTARIOS: Cuando la suma de dos ángulos es igual a noventa grados.

3.      ANGULOS SUPLEMENTARIOS: Cuando la suma de dos ángulos es igual a ciento ochenta grados.

4.      ANGULOS CONSECUTIVOS: Cuando un ángulo tiene un lado y el origen común con otro ángulo.

5.      ANGULO CONVEXO: Esta comprendido entre los lados o semirrectas de un ángulo.

② PAREO. Sobre el espacio de la columna izquierda, escribe el número correspondiente de la columna derecha.

__9__ Angulo agudo                                                                 1.Transportados

_ 12_ Angulo Suplementarios                                                    3.Mide 360º

_ 10_ Angulos consecutivos                                                       4.Angulo

__4__ Dos semirrectas con origen comun                                  5.Su suma mide 90º

_ 15_ Angulo llano                                                                      6.

 _ no_ Un grado                                                                           7. Vertice

__8__ Angulo obtuso                                                                   8.159º

__5__ Angulos complementarios                                                 9.74º

__ 3_ Angulo de giro                                                                    10.Un lado y origen común.

_  7_ Origenes del lado del angulo                                                11.  

_ 13_ Angulo convexo                                                                   12.Su suma mide 180º

__ 1_ Instrumentos para medir angulos                                        13.Comprendido entre lados de angulo

_ no_ Formula para transformar de angulos                                  14.1/360 de circunfer       

 a radianes.                                                                                           

 _ no_ Formula para transformar de                                               15.Mide 180º

radianes a grados                                                                                 

Nitzia González. 8-475-1000.

El Juego de Geometría

Durante el estudio de la geometría debemos hacer uso de ciertos instrumentos geométricos que nos facilitan el trazado de figuras, líneas, medición de ángulos, etc.

A. Instrumentos

Al conjunto de esos instrumentos se le conoce como juego de Geometría y, generalmente, esta compuesto por:

1. Una regla

2. Una escuadra de 45%

3. Una escuadra 60% y 30%

4. Un compás

5. Un transportador

1. La regla (gráfico No. 53)

La regla sirve para trazar líneas y para medir segmentos. La regla está graduada por un lado en centímetros, y por el otro, en pulgadas.

 (gráfico No. 53)

2. La escuadra de 45° (gráfico No.54)

Recibe este nombre, porque dos de sus ángulos miden 45°. El otro, siempre es un ángulo recto.

Este instrumento es útil en la medición de ángulos de 45° y de 90°; también, en el trazado de paralelas y perpendiculares.

 (gráfico No. 54)

3. La escuadra de 60° y 30°

Recibe este nombre, porque sus otros ángulos son distintos del ángulos recto; uno mide 60° y otro 30°.

Este instrumento es útil en la medición de ángulos de 60°, 30° y 90°; como lo es también para el trazado de paralelas, perpendiculares y para el trazado de otras líneas. (Gráfico No. 55).

(gráfico No. 55)

4. El compás

Este instrumento sirve para trazar circunferencia y arcos de circunferencia. (Gráfico No. 56)

 (gráfico No. 56)

5. El transportador

Sirve para medir ángulos. (Gráfico No. 57)

 (gráfico No. 57)

B. USO DEL JUEGO DE GEOMETRÍA

Usos más comunes de los instrumentos geométricos

1. Trazado de una perpendicular a un segmento dado

a. Usando la regla y el transportador:

Primero traza una línea de trabajo sobre el cual marcarás el segmento ÃB, y en éste, un punto P sobre el que se va a levantar la perpendicular, así:

Hecho esto, coloca sobre líneas el transportador, haciendo que el punto de intersección de las líneas 0° a 180° y de la que viene de 90°, coincida con el punto P; marca entonces, un punto Q sobre los 90°, así:

Retira el transportador y une el punto Q con el punto P, resulta ya trazada una línea PQ que es perpendicular al segmento ÃB. (Gráfico No. 58)

b. Usando la regla y una escuadra

Trazada la línea de trabajo y marcado el punto P, coloca la escuadra (cualquiera de las dos), de manera que un ángulo recto coincida con el punto P sobre la línea ÃB; traza entonces el punto O sobre la línea que demarca la escuadra sobre P, así:

Une el punto O con el punto P y resulta que ÕP es perpendicular a ÃB. (Gráfico No. 59)

 

c. Usando la regla y el compás

Trazado el segmento ÃB y marcando el punto P, abre el compás con una amplitud moderada, preferiblemente menor que ÃP y haciendo centro en P, marca dos arcos E y F en ÃB así:

Abre ahora el compás con una amplitud mayor que ÃP y haciendo centro en E, traza un arco en el plano superior de ÃB; luego haz centro en F y traza otro arco en el mismo plano, de manera que se corte con el arco anterior, determinado así un punto O en la intersección de los arcos.

Traza un segmento que una los puntos O y P con el resultado de que ÕP es perpendicular a ÃB. (Gráfico No. 60)

d. Trazar una perpendicular como una amplitud un poco mayor que la distancia entre C y ÃB y traza desde C un arco que interseque a ÃB en E y F, así:

Abre ahora el compás con una amplitud mayor que la mitad de ÊF, haciendo centro en E marca un arco en el plano inferior de ÃB y centrando en F, marca otro arco en el mismo plano de manera que se intersequen, determinando el punto P.

Traza el segmento que une a C con P y resulta que CP * ÃB. (Gráfico No. 61)

2. Trazado de paralelas

a. Usando una regla:

Primero traza una paralela a una recta ÃB, desde un punto P fuera de la recta.

Toma la regla y mide la distancia perpendicular de P a la recta ÃB, así:

Mueve la regla a un lado del punto P y con la misma medida, marca otro punto que llamarás Q, así:

Luego, une los puntos P y Q para obtener una recta PQ que es paralela a la recta ÃB. (Gráfico No. 62)

b. Usando dos escuadras o una regla y una escuadra:

Coloca una escuadra de manera que uno de los bordes que forman el ángulo recto, coincida con la recta ÃB, así:

Luego, coloca la regla o la otra escuadra haciendo coincidir uno de sus bordes con el otro borde de la escuadra que está sobre ÃB y con el punto P, en la siguiente forma:

Hecho esto, mueve hacia arriba la primera escuadra hasta el punto P, y marca un punto Q en la línea que desmarca el borde de dicha escuadra. (Evita cualquier movimiento de la otra escuadra o regla para obtener una buena construcción).

Une los puntos P y Q para obtener la línea PQ que resulta ser paralelas a la recta ÃB. (Gráfico No. 63)

Es esta construcción, tal como lo hemos indicado en el proceso, puede reemplazarse la segunda escuadra por una regla, como se observa abajo y el resultado es el mismo.

NATALIA CEDEÑO 

8-901-1357

ENRIQUE ORTEGA

Dada la recta MN y un punto Q exterior a ella, traza una perpendicular del punto a la recta, utilizando las escuadras.

Dada la recta EF y el punto G exterior a ella, traza una paralela a la recta por el punto G, utilizando el compaz.

Desde una recta AB y dos puntos C, D, exteriores a ella, traza por el punto C una paralela a la recta y por el punto D, una perpendicular a la misma. Utiliza el método que te sea mas facil.

Dada una recta PQ y un punto R marcado el ella, traza una perpendicular que pase por R.

Sólo con el compás y una regla regla, traza una recta através de x que sea pralela a m. 

② identifica los siguientes triángulos atendiendo a sus anglos.

      

a) Triangulo rectángulo.   b) Triangulo obtusángulo.   c) Triangulo acutángulo.

③ identifica los siguientes triángulos atendiendo a sus lados.

              

a) Triangulo isósceles.          b) Triángulo equilátero.     c) Triangulo escaleno.

④ E la siguiente figura, identifica:

a)     Triángulos acutángulos:<E +<C +<D

b)    Triángulos obtusángulos:<E +<A +<D

c)     Triangulo rectángulos: <E +<A +<B

 Gabriela Cañate. 8-885-1020. 

Medimos en cada una de las líneas trazadas dos lados del acutángulo y marcamos los puntos C y H, luego haciendo centro en éstos, volvemos a medir 135 grados, de la misma manera que en el paso anterior.

Trazamos los lados que continúan  marcamos con D y G los nuevos puntos y desde los mimos, volvemos a medir 135 grados.

Trazamos dos nuevos lados y marcamos los puntos E y F, unimos estos puntos y obtenemos el acutángulo regular ABCDEFGH de 3 centímetros de lado.

Polígono irregular: es aquel que no tiene sus lados iguales, es decir, que no es equilátero.

El polígono irregular por tener lados desiguales, también tendrá ángulos desiguales.

Gabriela Cañate. 8-885-1020.


EL TRIANGULO 

Objetivos:
1.   Identificar los triángulos según sus lados y según sus ángulos.
2.   Construir diferentes tipos de triángulos.

Definición:  Es la porción de un plano limitado por tres rectas que se cortan dos a dos.

Los puntos de interseción de las tres rectas que se cortan formado el triángulo, se denominan vértices. En un triángulo,los vértices se designan por medio de letras mayusculas, ( A,B,C ) y los lados, por medio de letras minúsculas (a,b,c). En terminos generales los angulos formados en un triangulo se expresan de la siguiente manera : angulo A,B,C; angulo A,C,B; angulo B,A,C.

Se  coloca en el medio la letra que corresponde al vertice del angulo .   Algunos autores distinguen los angulos con las letras que les corresponden a los vertices respectivos .   Angulo A, angulo B, angulo C.   En el triangulo se distinguen angulos interno y externos.

Los angulos interno se denominan con la letra que corresponde al vertice:  A,B y C.   Los angulo externo estan formado  por  un lado y la prolongacion del otro .

La suma de la longitud de los tres lado de un triangulo recibe el nombre de perimetro.  Perimetro = segmento AB+ segmento BC + segmento AC.

El perimetro es una medida longitudinal que indica la medida del contorno de una figura geometrica cerrada plana.

 En un triangulo, el lado sobre el cual descansa la figura recibe el nombre de base ; el unico lado que recibe un nombre especial es este .

¿ Como se costruye un triangulo ?
Dado tres segmento ; x,y,z, un triangulo se construye de la siguiente  forma:
x                                                             y                                                 z
I_______________I   I_________________I           I______________I

1.   Con el compas medimos el segmento y, y trazamos una linea que tenga esa longitud .
2.   Luego , siempre usando el compas, medimos el segmento x, colocamos la punta del instrumento en un extremo del segmento y; se traza un arco de la circunferencia con radio igual al segmento x.
3.   Se mide la longitud del segmento z; ahora colocamos nuvamente la punta del instrumento, pero en el otro extremo del segmento y; se traza un arco de la circunferencia con radio igual al segmento z.
4.   Unimos cada extremo del segmento y con algunos de los dos puntos donde se cruzan los dos arcos trazados.

Para que tres segmento sean lados de un triangulo, debe cumplirse la siguiente propiedad :
La suma de las medidas de cualquier par de ellos debe ser mayor que la medida del otro lado.
Se conoce esta propiedad como desigualdad triangular.
x+y>z   x+z>y   y+z>x

YARIDETH TORIBIO
cedula : 3-705-1207



Clasificación de los triángulos atendiendo a sus lados

Atendiendo a sus lados, los  triángulos se clasifican en .

triangulo isósceles

es aquel que tiene dos de sus lados iguales . En este triangulo , los ángulos opuestos a los lados  iguales , también son iguales . Se verifica que. AC es igual a BC

 

 

 

 

Construir un triangulo isósceles de 4 cm de base y cuyos lados iguales midan 6 cm .

Trazas la línea de trabajo .levantas la perpendicular PQ desde el Q mides 2 cm de cada lado y marcas A y B

 

 

Hecho lo anterior , mides desde B hasta el lado derecho de PQ, 6 cm .

 

 

 

Unes A con C y resulta el triangulo isósceles ABC con las medidas deseadas .